Survival analysis: Cox proportional hazards model

TODO

  • link to survivalKM, survivalParametric

Install required packages

survival

wants <- c("survival")
has   <- wants %in% rownames(installed.packages())
if(any(!has)) install.packages(wants[!has])

Simulated right-censored event times with Weibull distribution

Time independent covariates with proportional hazards

\(T = (-\ln(U) \, b \, e^{-\bf{X} \bf{\beta}})^{\frac{1}{a}}\), where \(U \sim \mathcal{U}(0, 1)\)

set.seed(123)
N      <- 180
P      <- 3
sex    <- factor(sample(c("f", "m"), N, replace=TRUE))
X      <- rnorm(N, 0, 1)
IV     <- factor(rep(LETTERS[1:P], each=N/P))
IVeff  <- c(0, -1, 1.5)
Xbeta  <- 0.7*X + IVeff[unclass(IV)] + rnorm(N, 0, 2)
weibA  <- 1.5
weibB  <- 100
U      <- runif(N, 0, 1)
eventT <- ceiling((-log(U)*weibB*exp(-Xbeta))^(1/weibA))
obsLen <- 120
censT  <- rep(obsLen, N)
obsT   <- pmin(eventT, censT)
status <- eventT <= censT
dfSurv <- data.frame(obsT, status, sex, X, IV)

Survival data in counting process (start-stop) notation.

library(survival)
dfSurvCP <- survSplit(dfSurv, cut=seq(30, 90, by=30), end="obsT",
                      event="status", start="start", id="ID", zero=0)

Fit the Cox proportional hazards model

Assumptions

\[ \begin{equation*} \begin{array}{rclcl} \ln \lambda(t) &=& \ln \lambda_{0}(t) + \beta_{1} X_{1} + \dots + \beta_{p} X_{p} &=& \ln \lambda_{0}(t) + \bf{X} \bf{\beta}\\ \lambda(t) &=& \lambda_{0}(t) \, e^{\beta_{1} X_{1} + \dots + \beta_{p} X_{p}} &=& \lambda_{0}(t) \, e^{\bf{X} \bf{\beta}}\\ S(t) &=& S_{0}(t)^{\exp(\bf{X} \bf{\beta})} &=& \exp\left(-\Lambda_{0}(t) \, e^{\bf{X} \bf{\beta}}\right)\\ \Lambda(t) &=& \Lambda_{0}(t) \, e^{\bf{X} \bf{\beta}} & & \end{array} \end{equation*} \]

library(survival)
(fitCPH <- coxph(Surv(obsT, status) ~ X + IV, data=dfSurv))
Call:
coxph(formula = Surv(obsT, status) ~ X + IV, data = dfSurv)

      coef exp(coef) se(coef)     z       p
X    0.493     1.637   0.0937  5.26 1.4e-07
IVB -0.822     0.439   0.2108 -3.90 9.6e-05
IVC  0.377     1.457   0.1934  1.95 5.1e-02

Likelihood ratio test=51.6  on 3 df, p=3.62e-11  n= 180, number of events= 157

Use counting process data format.

coxph(Surv(start, obsT, status) ~ X + IV, data=dfSurvCP)
summary(fitCPH)
# not shown

Assess model fit

AIC

library(survival)
extractAIC(fitCPH)
[1]    3.000 1367.667

McFadden, Cox & Snell and Nagelkerke pseudo \(R^{2}\)

Log-likelihoods for full model and 0-model without predictors X1, X2

LLf <- fitCPH$loglik[2]
LL0 <- fitCPH$loglik[1]

McFadden pseudo-\(R^2\)

as.vector(1 - (LLf / LL0))
[1] 0.0365218

Cox & Snell

as.vector(1 - exp((2/N) * (LL0 - LLf)))
[1] 0.2493033

Nagelkerke

as.vector((1 - exp((2/N) * (LL0 - LLf))) / (1 - exp(LL0)^(2/N)))
[1] 0.2494003

Model comparisons

Restricted model without factor IV

library(survival)
fitCPH1 <- coxph(Surv(obsT, status) ~ X, data=dfSurv)
anova(fitCPH1, fitCPH)          # model comparison
Analysis of Deviance Table
 Cox model: response is  Surv(obsT, status)
 Model 1: ~ X
 Model 2: ~ X + IV
   loglik  Chisq Df P(>|Chi|)    
1 -698.77                        
2 -680.83 35.867  2 1.628e-08 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Estimate survival-function und cumulative baseline hazard

Survival function

For average pseudo-observation with covariate values equal to the sample means. For factors: means of dummy-coded indicator variables.

library(survival)                # for survfit()
(CPH <- survfit(fitCPH))
Call: survfit(formula = fitCPH)

records   n.max n.start  events  median 0.95LCL 0.95UCL 
    180     180     180     157      14      11      19 
quantile(CPH, probs=c(0.25, 0.5, 0.75), conf.int=FALSE)
25 50 75 
 4 14 39

More meaningful: Estimated survival function for new specific data

dfNew  <- data.frame(sex=factor(c("f", "f"), levels=levels(dfSurv$sex)),
                       X=c(-2, -2),
                      IV=factor(c("A", "C"), levels=levels(dfSurv$IV)))

library(survival)
CPHnew <- survfit(fitCPH, newdata=dfNew)

par(mar=c(5, 4.5, 4, 2)+0.1, cex.lab=1.4, cex.main=1.4)
plot(CPH, main=expression(paste("Cox PH-estimate ", hat(S)(t), " with CI")),
     xlab="t", ylab="Survival", lwd=2)
lines(CPHnew$time, CPHnew$surv[ , 1], lwd=2, col="blue")
lines(CPHnew$time, CPHnew$surv[ , 2], lwd=2, col="red")
legend(x="topright", lwd=2, col=c("black", "blue", "red"),
       legend=c("pseudo-observation", "sex=f, X=-2, IV=A", "sex=f, X=-2, IV=C"))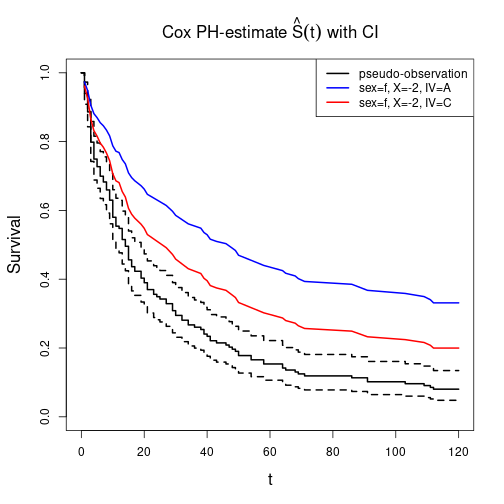
plot of chunk rerSurvivalCoxPH01

Cumulative baseline hazard

library(survival)                # for basehaz()
expCoef  <- exp(coef(fitCPH))
Lambda0A <- basehaz(fitCPH, centered=FALSE)
Lambda0B <- expCoef[2]*Lambda0A$hazard
Lambda0C <- expCoef[3]*Lambda0A$hazard
plot(hazard ~ time, main=expression(paste("Cox PH-estimate ", hat(Lambda)[g](t), " per group")),
     type="s", ylim=c(0, 5), xlab="t", ylab="cumulative hazard", lwd=2, data=Lambda0A)
lines(Lambda0A$time, Lambda0B, lwd=2, col="red")
lines(Lambda0A$time, Lambda0C, lwd=2, col="green")
legend(x="bottomright", lwd=2, col=1:3, legend=LETTERS[1:3])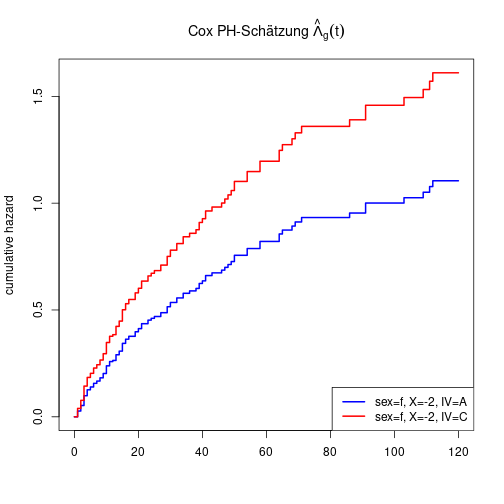
plot of chunk rerSurvivalCoxPH02

Model diagnostics

Proportional hazards assumption

log-log plot for categorized predictor X.

library(survival)                # for survfit()
dfSurv <- transform(dfSurv, Xcut=cut(X, breaks=c(-Inf, median(X), Inf),
                                        labels=c("lo", "hi")))
KMiv   <- survfit(Surv(obsT, status) ~ IV,   type="kaplan-meier", data=dfSurv)
KMxcut <- survfit(Surv(obsT, status) ~ Xcut, type="kaplan-meier", data=dfSurv)

plot(KMiv, fun="cloglog", main="cloglog-Plot for IV1", xlab="ln t",
     ylab=expression(ln(-ln(hat(S)[g](t)))), col=c("black", "blue", "red"), lty=1:3)

legend(x="topleft", col=c("black", "blue", "red"), lwd=2, lty=1:3, legend=LETTERS[1:3])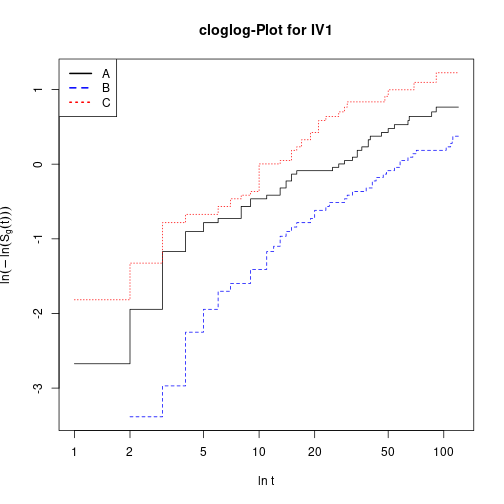
plot of chunk rerSurvivalCoxPH03
plot(KMxcut, fun="cloglog", main="cloglog-Plot for Xcut", xlab="ln t",
     ylab=expression(ln(-ln(hat(S)[g](t)))), col=c("black", "blue"), lty=1:2)

legend(x="topleft", col=c("black", "blue"), lwd=2, lty=1:2, legend=c("lo", "hi"))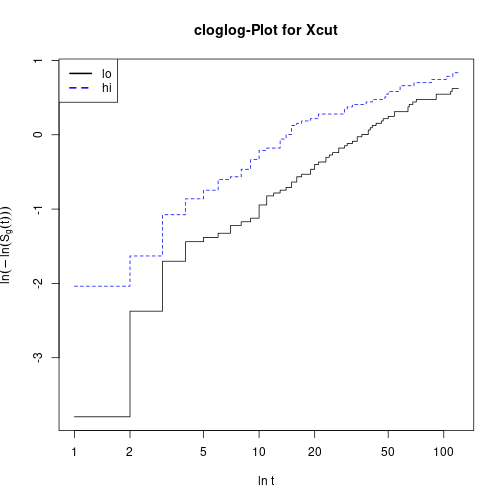
plot of chunk rerSurvivalCoxPH03

Test based on scaled Schoenfeld-residuals

library(survival)                      # for cox.zph()
(czph <- cox.zph(fitCPH))
           rho chisq      p
X      -0.1039 2.073 0.1500
IVB     0.1559 4.006 0.0453
IVC     0.0406 0.265 0.6069
GLOBAL      NA 5.053 0.1680

Plot scaled Schoenfeld-residuals against covariates

par(mfrow=c(2, 2), cex.main=1.4, cex.lab=1.4)
plot(czph)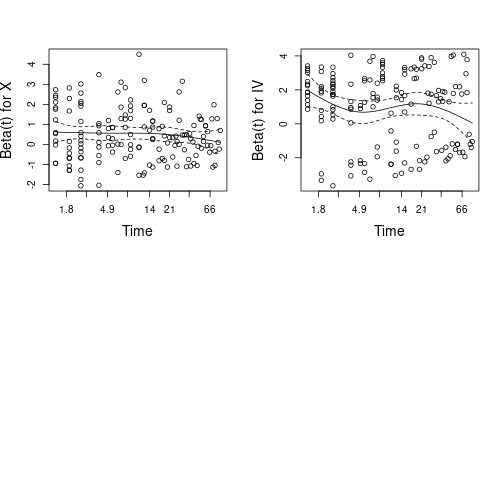
plot of chunk rerSurvivalCoxPH04

Influential observations

dfbetas <- residuals(fitCPH, type="dfbetas")

par(mfrow=c(2, 2), cex.main=1.4, cex.lab=1.4)
plot(dfbetas[ , 1], type="h", main="DfBETAS for X",    ylab="DfBETAS", lwd=2)
plot(dfbetas[ , 2], type="h", main="DfBETAS for IV-B", ylab="DfBETAS", lwd=2)
plot(dfbetas[ , 3], type="h", main="DfBETAS for IV-C", ylab="DfBETAS", lwd=2)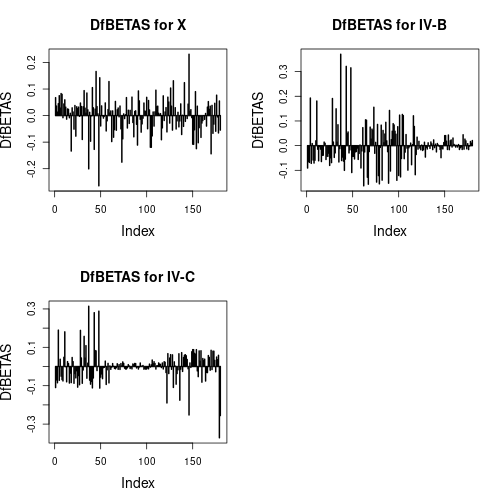
plot of chunk rerSurvivalCoxPH05

Linearity of log hazard

Plot martingale-residuals against continuous covariate with a nonparametric LOESS-smoother

resMart <- residuals(fitCPH, type="martingale")
plot(dfSurv$X, resMart, main="Martingale-residuals for X",
     xlab="X", ylab="Residuen", pch=20)
lines(loess.smooth(dfSurv$X, resMart), lwd=2, col="blue")
legend(x="bottomleft", col="blue", lwd=2, legend="LOESS fit", cex=1.4)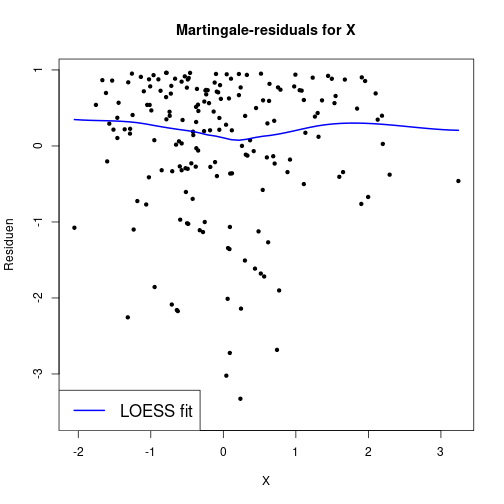
plot of chunk rerSurvivalCoxPH06

Predicted hazard ratios

With respect to an average pseudo-observation with covariate values equal to the sample means. For factors: means of dummy-coded indicator variables.

library(survival)
predRes <- predict(fitCPH, type="risk")
head(predRes, n=10)
 [1] 1.9166403 1.5389801 1.3210722 0.8617067 2.2969713 0.8735328 3.4527637
 [8] 2.5002058 1.0455378 0.7079919

Estimated global survival function.

library(survival)
Shat1 <- survexp(~ 1, ratetable=fitCPH, data=dfSurv)
with(Shat1, head(data.frame(time, surv), n=4))
  time      surv
1    1 0.9269729
2    2 0.8643413
3    3 0.7681378
4    4 0.7173365

Estimated survival function per group.

library(survival)
Shat2 <- survexp(~ IV, ratetable=fitCPH, data=dfSurv)
with(Shat2, head(data.frame(time, surv), n=4))
  time      IV.A      IV.B      IV.C
1    1 0.9265656 0.9633824 0.8909708
2    2 0.8626937 0.9299972 0.8003328
3    3 0.7630677 0.8746553 0.6666905
4    4 0.7097748 0.8431836 0.5990511

Further resources

For Cox PH models with Firth’s penalized likelihood, see package coxphf.

Detach (automatically) loaded packages (if possible)

try(detach(package:survival))
try(detach(package:splines))

Get the article source from GitHub

R markdown - markdown - R code - all posts

top

© 2020 Daniel Wollschlaeger - licensed under CC-BY-SA Creative Commons BY-SA