Nonparametric bootstrapping linear models

TODO

• GLM example
• link to resamplingBoot

Install required packages

boot

wants <- c("boot")
has   <- wants %in% rownames(installed.packages())
if(any(!has)) install.packages(wants[!has])

Regression parameters: Case resampling

set.seed(123)
N  <- 100
X1 <- rnorm(N, 175, 7)
X2 <- rnorm(N,  30, 8)
X3 <- abs(rnorm(N, 60, 30))
Y  <- 0.5*X1 - 0.3*X2 - 0.4*X3 + 10 + rnorm(N, 0, 3)
dfRegr <- data.frame(X1, X2, X3, Y)

(fit <- lm(Y ~ X1 + X2 + X3, data=dfRegr))

Call:
lm(formula = Y ~ X1 + X2 + X3, data = dfRegr)

Coefficients:
(Intercept)           X1           X2           X3  
    13.9252       0.4762      -0.2827      -0.4057  

sqrt(diag(vcov(fit)))

(Intercept)          X1          X2          X3 
 9.05357721  0.05008996  0.04104598  0.01122308 

confint(fit)

                 2.5 %     97.5 %
(Intercept) -4.0460232 31.8963943
X1           0.3768077  0.5756632
X2          -0.3641438 -0.2011926
X3          -0.4280163 -0.3834611

getRegr <- function(dat, idx) {
    bsFit <- lm(Y ~ X1 + X2 + X3, subset=idx, data=dat)
    coef(bsFit)
}

library(boot)
nR <- 999
(bsRegr <- boot(dfRegr, statistic=getRegr, R=nR))

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = dfRegr, statistic = getRegr, R = nR)


Bootstrap Statistics :
      original        bias    std. error
t1* 13.9251855 -0.4537363444  7.74596234
t2*  0.4762354  0.0026731851  0.04289680
t3* -0.2826682 -0.0002800234  0.04108043
t4* -0.4057387  0.0002494345  0.01197575

boot.ci(bsRegr, conf=0.95, type="bca", index=1)$bca

     conf                                
[1,] 0.95 26.48 976.31 -1.756034 28.90993

boot.ci(bsRegr, conf=0.95, type="bca", index=2)$bca

     conf                                 
[1,] 0.95 24.26 974.17 0.3938218 0.5655422

boot.ci(bsRegr, conf=0.95, type="bca", index=3)$bca

     conf                                
[1,] 0.95 24.04 974 -0.3663432 -0.2021897

boot.ci(bsRegr, conf=0.95, type="bca", index=4)$bca

     conf                                   
[1,] 0.95 18.29 966.64 -0.4307008 -0.3833435

ANOVA

Model-based resampling

Under the null hypothesis

P     <- 4
Nj    <- c(41, 37, 42, 40)
muJ   <- rep(c(-1, 0, 1, 2), Nj)
dfCRp <- data.frame(IV=factor(rep(LETTERS[1:P], Nj)),
                    DV=rnorm(sum(Nj), muJ, 6))

anBase <- anova(lm(DV ~ IV, data=dfCRp))
Fbase  <- anBase["IV", "F value"]
(pBase <- anBase["IV", "Pr(>F)"])

[1] 0.2748375

fit0 <- lm(DV ~ 1, data=dfCRp)        ## fit 0-model
E    <- residuals(fit0)               ## residuals
Er   <- E / sqrt(1-hatvalues(fit0))   ## rescaled residuals
Yhat <- fitted(fit0)                  ## prediction

getAnova <- function(dat, idx) {
    Ystar <- Yhat + Er[idx]
    anBS  <- anova(lm(Ystar ~ IV, data=dat))
    anBS["IV", "F value"]
}

library(boot)
nR       <- 999
(bsAnova <- boot(dfCRp, statistic=getAnova, R=nR))

ORDINARY NONPARAMETRIC BOOTSTRAP


Call:
boot(data = dfCRp, statistic = getAnova, R = nR)


Bootstrap Statistics :
    original     bias    std. error
t1* 1.304972 -0.3013633   0.8547824

Fstar    <- bsAnova$t

# don't use >= because of floating point arithmetic problems
tol     <- .Machine$double.eps^0.5
FsIsGEQ <- (Fstar > Fbase) | (abs(Fstar-Fbase) < tol)
(pValBS <- (sum(FsIsGEQ) + 1) / (length(Fstar) + 1))

[1] 0.266

plot(Fstar, ecdf(Fstar)(Fstar), col="gray60", pch=1, xlab="f* bzw. f",
     ylab="P(F <= f)", main="F*: cumulative rel. freqs and F CDF")
curve(pf(x, P-1, sum(Nj) - P), lwd=2, add=TRUE)
legend(x="topleft", lty=c(NA, 1), pch=c(1, NA), lwd=c(2, 2),
       col=c("gray60", "black"), legend=c("F*", "F"))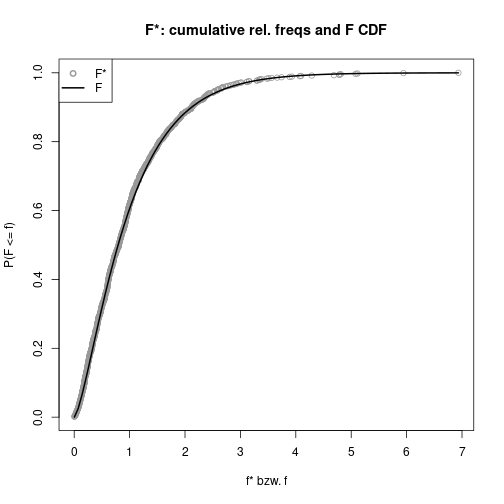

Wild boostrap

Under the null hypothesis

getAnovaWild <- function(dat, idx) {
    n  <- length(idx)                     ## size of replication
    ## 1st choice for random variate U: Rademacher-variables
    Ur <- sample(c(-1, 1), size=n, replace=TRUE, prob=c(0.5, 0.5))

    ## 2nd option for choosing random variate U
    Uf <- sample(c(-(sqrt(5) - 1)/2, (sqrt(5) + 1)/2), size=n, replace=TRUE,
                 prob=c((sqrt(5) + 1)/(2*sqrt(5)), (sqrt(5) - 1)/(2*sqrt(5))))

    Ystar <- Yhat + (Er*Ur)[idx]          ## for E* with Rademacher-variables
    # Ystar <- Yhat + (Er*Uf)[idx]        ## for E* with 2nd option
    anBS  <- anova(lm(Ystar ~ IV, data=dat))
    anBS["IV", "F value"]
}

library(boot)
nR       <- 999
bsAnovaW <- boot(dfCRp, statistic=getAnovaWild, R=nR)
FstarW   <- bsAnovaW$t

# don't use >= because of floating point arithmetic problems
tol      <- .Machine$double.eps^0.5
FsIsGEQ  <- (FstarW > Fbase) | (abs(FstarW-Fbase) < tol)
(pValBSw <- (sum(FsIsGEQ) + 1) / (length(FstarW) + 1))

[1] 0.251

Detach (automatically) loaded packages (if possible)

try(detach(package:boot))

Get the article source from GitHub

R markdown - markdown - R code - all posts