Robust and penalized regression
TODO
- link to regression, resamplingBootALM
Install required packages
glmnet, lmtest, MASS, robustbase, sandwich
wants <- c("glmnet", "lmtest", "MASS", "robustbase", "sandwich")
has <- wants %in% rownames(installed.packages())
if(any(!has)) install.packages(wants[!has])Robust regression
Simulate data.
set.seed(123)
N <- 100
X1 <- rnorm(N, 175, 7)
X2 <- rnorm(N, 30, 8)
X3 <- abs(rnorm(N, 60, 30))
Y <- 0.5*X1 - 0.3*X2 - 0.4*X3 + 10 + rnorm(N, 0, 7)
dfRegr <- data.frame(X1, X2, X3, Y)Using ltsReg() from package robustbase
Least trimmed squares regression.
library(robustbase)
ltsFit <- ltsReg(Y ~ X1 + X2 + X3, data=dfRegr)
summary(ltsFit)
Call:
ltsReg.formula(formula = Y ~ X1 + X2 + X3, data = dfRegr)
Residuals (from reweighted LS):
Min 1Q Median 3Q Max
-16.81677 -5.06892 -0.04087 4.32097 16.62449
Coefficients:
Estimate Std. Error t value Pr(>|t|)
Intercept 16.42589 20.18060 0.814 0.4177
X1 0.45579 0.11165 4.082 9.36e-05 ***
X2 -0.18335 0.09196 -1.994 0.0491 *
X3 -0.42834 0.02505 -17.101 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 7.02 on 94 degrees of freedom
Multiple R-Squared: 0.783, Adjusted R-squared: 0.7761
F-statistic: 113.1 on 3 and 94 DF, p-value: < 2.2e-16 Using rlm() from package MASS
\(M\)-estimators.
library(MASS)
fitRLM <- rlm(Y ~ X1 + X2 + X3, data=dfRegr)
summary(fitRLM)
Call: rlm(formula = Y ~ X1 + X2 + X3, data = dfRegr)
Residuals:
Min 1Q Median 3Q Max
-17.7418 -4.9231 0.3231 4.8329 17.7265
Coefficients:
Value Std. Error t value
(Intercept) 16.1951 21.9427 0.7381
X1 0.4573 0.1214 3.7668
X2 -0.2336 0.0995 -2.3478
X3 -0.4127 0.0272 -15.1709
Residual standard error: 7.248 on 96 degrees of freedomFor resistant regression, see lqs() from package MASS.
Heteroscedasticity-consistent standard errors
Heteroscedasticity-consistent standard errors (modified White estimator): hccm() from package car as well as vcovHC() from package sandwich. Sandwich estimator from sandwich() from the eponymous package. These standard errors can then be used in combination with function coeftest() from package lmtest().
fit <- lm(Y ~ X1 + X2 + X3, data=dfRegr)
library(sandwich)
hcSE <- vcovHC(fit, type="HC3")
library(lmtest)
coeftest(fit, vcov=hcSE)
t test of coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 19.158766 19.553515 0.9798 0.329642
X1 0.444549 0.108464 4.0986 8.694e-05 ***
X2 -0.259559 0.095858 -2.7077 0.008021 **
X3 -0.413390 0.028283 -14.6160 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Penalized regression
Fit penalized models on standardized data.
Ridge regression
Using lm.ridge() from package MASS.
Calculate estimated prediction error from generalized crossvalidation (GCV) for a range of values for regularization parameter \(\lambda\).
library(MASS)
lambdas <- 10^(seq(-2, 4, length=100))
ridgeGCV <- lm.ridge(scale(Y) ~ scale(X1) + scale(X2) + scale(X3),
data=dfRegr, lambda=lambdas)Show value for \(\lambda\) with minimal GCV error and get parameter estimates for this choice.
select(ridgeGCV)modified HKB estimator is 0.3627288
modified L-W estimator is 0.3387983
smallest value of GCV at 1.149757 ridgeSel <- lm.ridge(scale(Y) ~ scale(X1) + scale(X2) + scale(X3),
lambda=1.50)
coef(ridgeSel) scale(X1) scale(X2) scale(X3)
3.571560e-16 1.928426e-01 -1.356254e-01 -7.934664e-01 Show estimated prediction error from GCV depending on regularization parameter \(\lambda\).
plot(x=log(ridgeGCV$lambda), y=ridgeGCV$GCV, main="Ridge",
xlab="log(lambda)", ylab="GCV")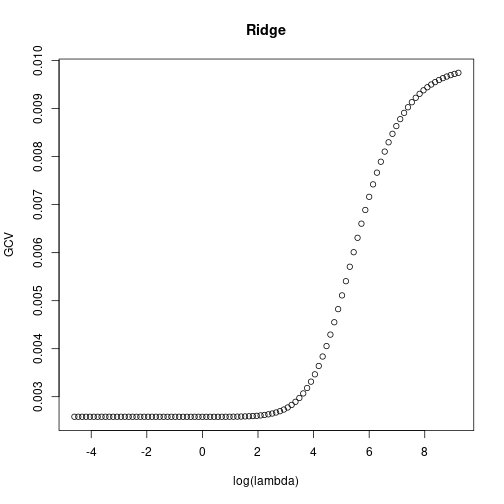
Using cv.glmnet() from package glmnet
cv.glmnet() has no formula interface, data has to be in matrix format. Set alpha=0 for ridge regression. First calculate GCV prediction error for a range of values for \(\lambda\).
library(glmnet)
matScl <- scale(cbind(Y, X1, X2, X3))
ridgeCV <- cv.glmnet(x=matScl[ , c("X1", "X2", "X3")], y=matScl[ , "Y"],
nfolds=10, alpha=0)Fit model for value of \(\lambda\) with minimal GCV prediction error using glmnet().
ridge <- glmnet(x=matScl[ , c("X1", "X2", "X3")], y=matScl[ , "Y"],
lambda=ridgeCV$lambda.min, alpha=0)
coef(ridge)4 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 3.687535e-16
X1 1.868438e-01
X2 -1.287210e-01
X3 -7.442521e-01Show regularization path (here: coefficients against \(\ln \lambda\).
plot(ridgeCV$glmnet.fit, xvar="lambda", label=TRUE, lwd=2)
title("Ridge", line=3, col="blue")
legend(x="bottomright", legend=c("X1", "X2", "X3"), lwd=2,
col=c("black", "red", "green"), bg="white")
LASSO
Set alpha=1 for LASSO.
lassoCV <- cv.glmnet(x=matScl[ , c("X1", "X2", "X3")], y=matScl[ , "Y"],
nfolds=10, alpha=1)
lasso <- glmnet(x=matScl[ , c("X1", "X2", "X3")], y=matScl[ , "Y"],
lambda=lassoCV$lambda.min, alpha=1)
coef(lasso)4 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 3.711313e-16
X1 1.909584e-01
X2 -1.337116e-01
X3 -8.018863e-01Show regularization path (here: coefficients against L1-norm).
plot(lassoCV$glmnet.fit, xvar="norm", label=FALSE, lwd=2)
title("LASSO", line=3, col="blue")
legend(x="bottomleft", legend=c("X1", "X2", "X3"), lwd=2,
col=c("black", "red", "green"), bg="white")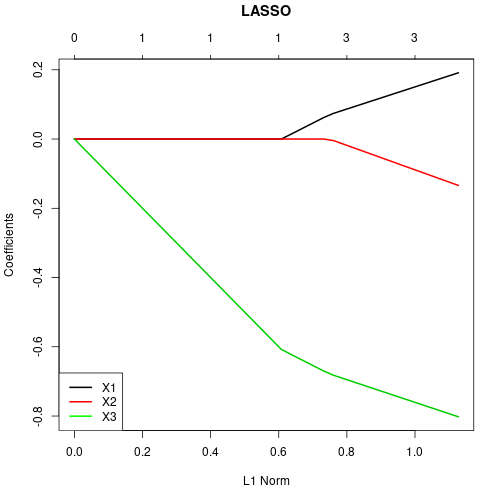
Elastic net
Set alpha=0.5 for elastic net.
elNetCV <- cv.glmnet(x=matScl[ , c("X1", "X2", "X3")], y=matScl[ , "Y"],
nfolds=10, alpha=0.5)
elNet <- glmnet(x=matScl[ , c("X1", "X2", "X3")], y=matScl[ , "Y"],
lambda=lassoCV$lambda.min, alpha=0.5)
coef(elNet)4 x 1 sparse Matrix of class "dgCMatrix"
s0
(Intercept) 3.726081e-16
X1 1.923908e-01
X2 -1.352724e-01
X3 -8.020281e-01Show regularization path (here: coefficients against deviance explained).
plot(elNetCV$glmnet.fit, xvar="dev", label=FALSE, lwd=2)
title("Elastic Net", line=3, col="blue")
legend(x="bottomleft", legend=c("X1", "X2", "X3"), lwd=2,
col=c("black", "red", "green"), bg="white")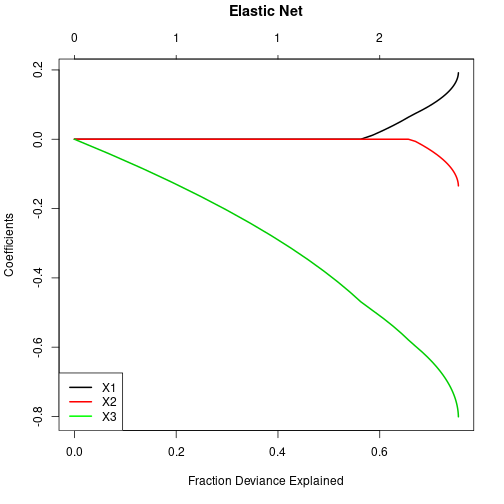
Further resources
More information can be found in CRAN task view Robust Statistical Methods.
Detach (automatically) loaded packages (if possible)
try(detach(package:lmtest))
try(detach(package:sandwich))
try(detach(package:zoo))
try(detach(package:glmnet))
try(detach(package:Matrix))
try(detach(package:robustbase))
try(detach(package:MASS))Get the article source from GitHub
R markdown - markdown - R code - all posts