Binary logistic regression
TODO
- link to associationOrder for
pROC, regressionOrdinal, regressionMultinom, regressionDiag for outliers, collinearity, crossvalidation
Install required packages
wants <- c("rms")
has <- wants %in% rownames(installed.packages())
if(any(!has)) install.packages(wants[!has])Descriptive model fit
Simulate data
set.seed(123)
SSRIpre <- c(18, 16, 16, 15, 14, 20, 14, 21, 25, 11)
SSRIpost <- c(12, 0, 10, 9, 0, 11, 2, 4, 15, 10)
PlacPre <- c(18, 16, 15, 14, 20, 25, 11, 25, 11, 22)
PlacPost <- c(11, 4, 19, 15, 3, 14, 10, 16, 10, 20)
WLpre <- c(15, 19, 10, 29, 24, 15, 9, 18, 22, 13)
WLpost <- c(17, 25, 10, 22, 23, 10, 2, 10, 14, 7)
P <- 3
Nj <- rep(length(SSRIpre), times=P)
IV <- factor(rep(1:P, Nj), labels=c("SSRI", "Placebo", "WL"))
DVpre <- c(SSRIpre, PlacPre, WLpre)
DVpost <- c(SSRIpost, PlacPost, WLpost)
postFac <- cut(DVpost, breaks=c(-Inf, median(DVpost), Inf),
labels=c("lo", "hi"))
dfAncova <- data.frame(IV, DVpre, DVpost, postFac)cdplot(postFac ~ DVpre, data=dfAncova, subset=IV == "SSRI",
main="Estimated categ probs SSRI")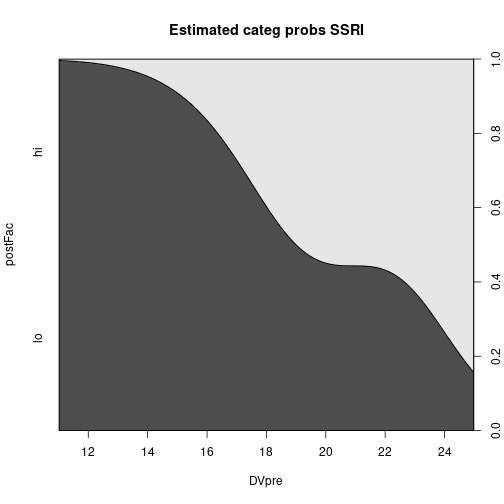
cdplot(postFac ~ DVpre, data=dfAncova, subset=IV == "Placebo",
main="Estimated categ probs placebo")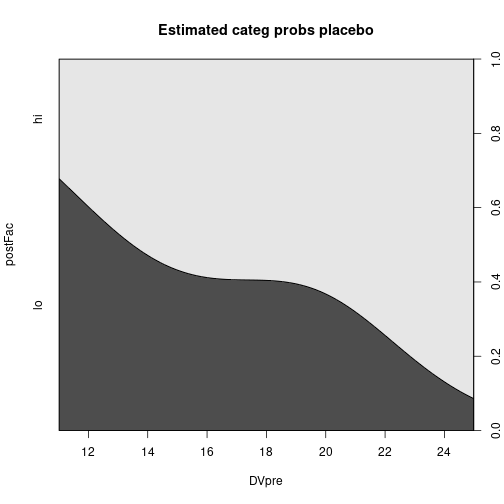
cdplot(postFac ~ DVpre, data=dfAncova, subset=IV == "WL",
main="Estimated categ probs WL")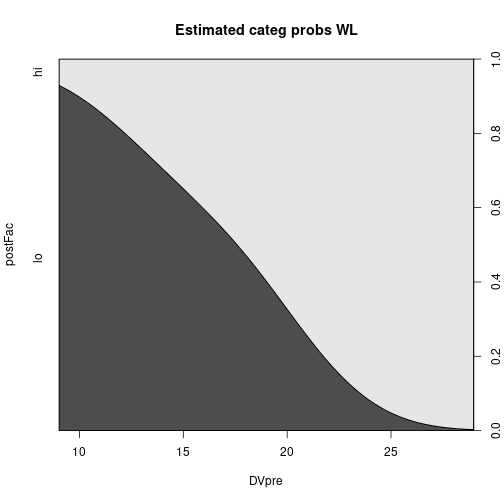
Fit the model
(glmFit <- glm(postFac ~ DVpre + IV, family=binomial(link="logit"), data=dfAncova))
Call: glm(formula = postFac ~ DVpre + IV, family = binomial(link = "logit"),
data = dfAncova)
Coefficients:
(Intercept) DVpre IVPlacebo IVWL
-8.4230 0.4258 1.7306 1.2027
Degrees of Freedom: 29 Total (i.e. Null); 26 Residual
Null Deviance: 41.46
Residual Deviance: 24.41 AIC: 32.41Odds ratios
exp(coef(glmFit)) (Intercept) DVpre IVPlacebo IVWL
0.0002197532 1.5308001795 5.6440022784 3.3291484767 Profile likelihood based confidence intervals for odds ratios
exp(confint(glmFit)) 2.5 % 97.5 %
(Intercept) 1.488482e-07 0.0251596
DVpre 1.193766e+00 2.2446549
IVPlacebo 5.343091e-01 95.1942030
IVWL 2.916673e-01 52.2883653Fit the model based on a matrix of counts
N <- 100
x1 <- rnorm(N, 100, 15)
x2 <- rnorm(N, 10, 3)
total <- sample(40:60, N, replace=TRUE)
hits <- rbinom(N, total, prob=0.4)
hitMat <- cbind(hits, total-hits)
glm(hitMat ~ x1 + x2, family=binomial(link="logit"))
Call: glm(formula = hitMat ~ x1 + x2, family = binomial(link = "logit"))
Coefficients:
(Intercept) x1 x2
-0.102410 -0.003373 0.005638
Degrees of Freedom: 99 Total (i.e. Null); 97 Residual
Null Deviance: 99.35
Residual Deviance: 96.44 AIC: 532.5Fit the model based on relative frequencies
relHits <- hits/total
glm(relHits ~ x1 + x2, weights=total, family=binomial(link="logit"))
Call: glm(formula = relHits ~ x1 + x2, family = binomial(link = "logit"),
weights = total)
Coefficients:
(Intercept) x1 x2
-0.102410 -0.003373 0.005638
Degrees of Freedom: 99 Total (i.e. Null); 97 Residual
Null Deviance: 99.35
Residual Deviance: 96.44 AIC: 532.5Fitted logits and probabilities
logitHat <- predict(glmFit, type="link")
plot(logitHat, pch=16, col=c("red", "blue")[unclass(dfAncova$postFac)])
abline(h=0)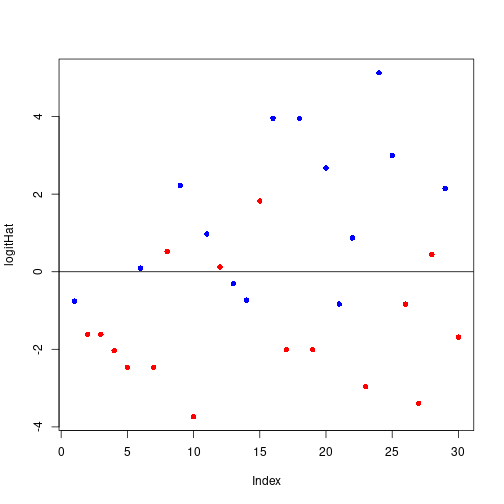
Phat <- fitted(glmFit)
Phat <- predict(glmFit, type="response")
head(Phat) 1 2 3 4 5 6
0.31891231 0.16653918 0.16653918 0.11545968 0.07856997 0.52318493 mean(Phat)[1] 0.4666667prop.table(xtabs(~ postFac, data=dfAncova))postFac
lo hi
0.5333333 0.4666667 Assess model fit
Classification table
thresh <- 0.5
facHat <- cut(Phat, breaks=c(-Inf, thresh, Inf), labels=c("lo", "hi"))
cTab <- xtabs(~ postFac + facHat, data=dfAncova)
addmargins(cTab) facHat
postFac lo hi Sum
lo 12 4 16
hi 4 10 14
Sum 16 14 30Correct classification rate
(CCR <- sum(diag(cTab)) / sum(cTab))[1] 0.7333333log-Likelihood, AUC, Somers’ \(D_{xy}\), Nagelkerke’s pseudo \(R^{2}\)
Deviance, log-likelihood and AIC
deviance(glmFit)[1] 24.40857logLik(glmFit)'log Lik.' -12.20428 (df=4)AIC(glmFit)[1] 32.40857Nagelkerke’s pseudo-\(R^{2}\) (R2), area under the ROC-Kurve (C), Somers’ \(D_{xy}\) (Dxy), Goodman & Kruskal’s \(\gamma\) (Gamma), Kendall’s \(\tau\) (Tau-a)
library(rms)
lrm(postFac ~ DVpre + IV, data=dfAncova)
Logistic Regression Model
lrm(formula = postFac ~ DVpre + IV, data = dfAncova)
Model Likelihood Discrimination Rank Discrim.
Ratio Test Indexes Indexes
Obs 30 LR chi2 17.05 R2 0.579 C 0.900
lo 16 d.f. 3 g 2.686 Dxy 0.799
hi 14 Pr(> chi2) 0.0007 gr 14.672 gamma 0.803
max |deriv| 2e-06 gp 0.404 tau-a 0.411
Brier 0.139
Coef S.E. Wald Z Pr(>|Z|)
Intercept -8.4230 2.9502 -2.86 0.0043
DVpre 0.4258 0.1553 2.74 0.0061
IV=Placebo 1.7306 1.2733 1.36 0.1741
IV=WL 1.2027 1.2735 0.94 0.3450 For plotting the ROC-curve, see pROC in associationOrder
McFadden, Cox & Snell and Nagelkerke pseudo \(R^{2}\)
Log-likelihoods for full model and 0-model without predictors X1, X2
N <- nobs(glmFit)
glm0 <- update(glmFit, . ~ 1)
LLf <- logLik(glmFit)
LL0 <- logLik(glm0)McFadden pseudo-\(R^2\)
as.vector(1 - (LLf / LL0))[1] 0.411209Cox & Snell
as.vector(1 - exp((2/N) * (LL0 - LLf)))[1] 0.4334714Nagelkerke
as.vector((1 - exp((2/N) * (LL0 - LLf))) / (1 - exp(LL0)^(2/N)))[1] 0.578822Crossvalidation
cv.glm() function from package boot, see crossvalidation
Apply model to new data
Nnew <- 3
dfNew <- data.frame(DVpre=rnorm(Nnew, 20, sd=7),
IV=factor(rep("SSRI", Nnew), levels=levels(dfAncova$IV)))
predict(glmFit, newdata=dfNew, type="response") 1 2 3
0.11516886 0.10427434 0.06270597 Coefficient tests and overall model test
Individual coefficient tests
Wald-tests for parameters
summary(glmFit)
Call:
glm(formula = postFac ~ DVpre + IV, family = binomial(link = "logit"),
data = dfAncova)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9865 -0.5629 -0.2372 0.4660 1.5455
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.4230 2.9502 -2.855 0.0043 **
DVpre 0.4258 0.1553 2.742 0.0061 **
IVPlacebo 1.7306 1.2733 1.359 0.1741
IVWL 1.2027 1.2735 0.944 0.3450
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 41.455 on 29 degrees of freedom
Residual deviance: 24.409 on 26 degrees of freedom
AIC: 32.409
Number of Fisher Scoring iterations: 5Or see lrm() above
Model comparisons - likelihood-ratio tests
anova(glm0, glmFit, test="Chisq")Analysis of Deviance Table
Model 1: postFac ~ 1
Model 2: postFac ~ DVpre + IV
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 29 41.455
2 26 24.409 3 17.047 0.0006912 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1drop1(glmFit, test="Chi")Single term deletions
Model:
postFac ~ DVpre + IV
Df Deviance AIC LRT Pr(>Chi)
<none> 24.409 32.409
DVpre 1 39.540 45.540 15.1319 0.0001003 ***
IV 2 26.566 30.566 2.1572 0.3400666
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Or see lrm() above
Model comparisons for testing IV
glmPre <- update(glmFit, . ~ . - IV) # no IV factor
anova(glmPre, glmFit, test="Chisq")Analysis of Deviance Table
Model 1: postFac ~ DVpre
Model 2: postFac ~ DVpre + IV
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 28 26.566
2 26 24.409 2 2.1572 0.3401Model comparisons for testing DVpre
anova(glm0, glmPre, test="Chisq")Analysis of Deviance Table
Model 1: postFac ~ 1
Model 2: postFac ~ DVpre
Resid. Df Resid. Dev Df Deviance Pr(>Chi)
1 29 41.455
2 28 26.566 1 14.89 0.000114 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Further resources
For penalized logistic regression, see packages logistf (using Firth’s penalized likelihood) and glmnet. An example using glmnet for linear regression is in regressionRobPen.
Detach (automatically) loaded packages (if possible)
try(detach(package:rms))
try(detach(package:Hmisc))
try(detach(package:grid))
try(detach(package:lattice))
try(detach(package:survival))
try(detach(package:splines))
try(detach(package:Formula))Get the article source from GitHub
R markdown - markdown - R code - all posts