Assess univariate and multivariate normality

Install required packages

energy, ICS, mvtnorm

wants <- c("energy", "ICS", "mvtnorm")
has   <- wants %in% rownames(installed.packages())
if(any(!has)) install.packages(wants[!has])

Univariate normality

QQ-plot

set.seed(123)
DV <- rnorm(20, mean=1.5, sd=3)
qqnorm(DV, pch=20, cex=2)
qqline(DV, col="gray60", lwd=2)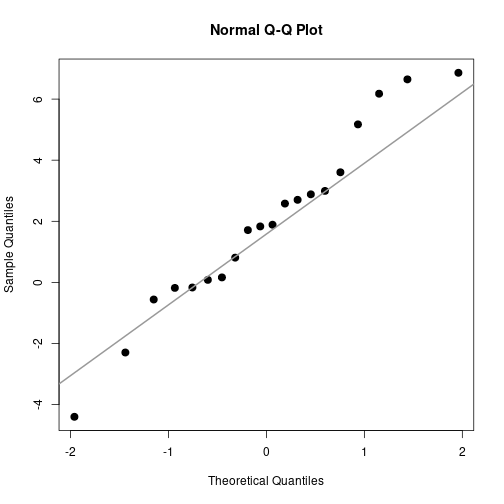

Shapiro-Wilk-test

Composite null hypothesis: any normal distribution

shapiro.test(DV)

    Shapiro-Wilk normality test

data:  DV
W = 0.9686, p-value = 0.7247

Anderson-Darling-test

Composite null hypothesis: any normal distribution

library(DescTools)
AndersonDarlingTest(DV)

    Anderson-Darling test of goodness-of-fit
    Null hypothesis: uniform distribution

data:  DV
An = Inf, p-value = 3e-05

Cramer-von-Mises-test

Composite null hypothesis: any normal distribution

library(DescTools)
CramerVonMisesTest(DV)

    Cramer-von Mises normality test

data:  DV
W = 0.038, p-value = 0.7014

Shapiro-Francia-test

Composite null hypothesis: any normal distribution

library(DescTools)
ShapiroFranciaTest(DV)

    Shapiro-Francia normality test

data:  DV
W = 0.9701, p-value = 0.6667

Jarque-Bera-test

Composite null hypothesis: any normal distribution

library(DescTools)
JarqueBeraTest(DV)

    Robust Jarque Bera Test

data:  DV
X-squared = 0.0183, df = 2, p-value = 0.9909

Kolmogorov-Smirnov-test

Exact null hypothesis: fully specified normal distribution

ks.test(DV, "pnorm", mean=1, sd=2, alternative="two.sided")

    One-sample Kolmogorov-Smirnov test

data:  DV
D = 0.239, p-value = 0.1726
alternative hypothesis: two-sided

Lilliefors-test

Composite null hypothesis: any normal distribution

library(DescTools)
LillieTest(DV)

    Lilliefors (Kolmogorov-Smirnov) normality test

data:  DV
D = 0.1071, p-value = 0.7925

Pearson \(\chi^{2}\)-test

Tests weaker null hypothesis (any distribution with the same probabilities for the given class intervals).

Wrong: pearson.test() does not use grouped ML-estimate or maximum \(\chi^{2}\)-estimate

library(DescTools)
PearsonTest(DV, n.classes=6, adjust=TRUE)

    Pearson chi-square normality test

data:  DV
P = 3.4, p-value = 0.334

Multivariate normality

Energy-test

mu    <- c(2, 4, 5)
Sigma <- matrix(c(4,2,-3, 2,16,-1, -3,-1,9), byrow=TRUE, ncol=3)
library(mvtnorm)
X <- rmvnorm(100, mu, Sigma)

library(energy)                    # for mvnorm.etest()
mvnorm.etest(X)

    Energy test of multivariate normality: estimated parameters

data:  x, sample size 100, dimension 3, replicates 999
E-statistic = 1.109, p-value = 0.03704

Kurtosis- and skew-test

Kurtosis-test

library(ICS)
mvnorm.kur.test(X)

    Multivariate Normality Test Based on Kurtosis

data:  X
W = 11.0848, w1 = 1.12, df1 = 5.00, w2 = 1.60, df2 = 1.00, p-value
= 0.1613

Skew-test

library(ICS)
X <- rmvnorm(100, c(2, 4, 5))
mvnorm.skew.test(X)

    Multivariate Normality Test Based on Skewness

data:  X
U = 2.6575, df = 3, p-value = 0.4475

Detach (automatically) loaded packages (if possible)

try(detach(package:DescTools))
try(detach(package:energy))
try(detach(package:ICS))
try(detach(package:mvtnorm))
try(detach(package:survey))
try(detach(package:CompQuadForm))

Get the article source from GitHub

R markdown - markdown - R code - all posts