Convex hull, (minimum) bounding box, and minimum enclosing circle
Convex hull
chull() returns the ordered indices of the matrix rows corresponding to corners of the convex hull.
set.seed(123)
xy <- matrix(rnorm(24, 100, 15), ncol=2)
hullIdx <- chull(xy)plot(xy, xlab="x", ylab="y", asp=1, type="n")
polygon(xy[hullIdx, ], border="blue", lwd=2)
points(xy, pch=16, cex=1.5)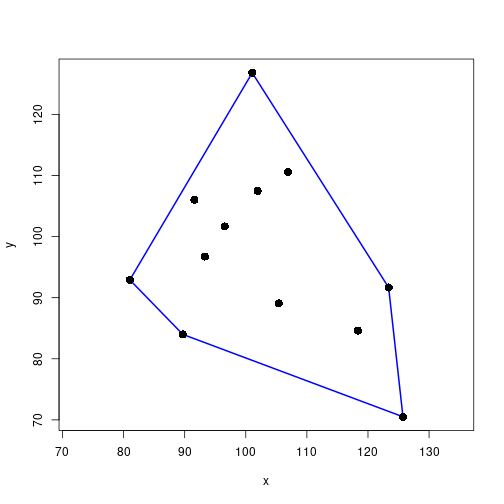
Bounding box
getBoundingBox <- function(xy) {
stopifnot(is.matrix(xy), is.numeric(xy), ncol(xy) == 2)
x <- range(xy[ , 1])
y <- range(xy[ , 2])
pts <- c(xleft=x[1], ybottom=y[1], xright=x[2], ytop=y[2])
return(list(pts=pts, width=abs(diff(x)), height=abs(diff(y))))
}bb <- getBoundingBox(xy)
plot(xy, xlab="x", ylab="y", asp=1, type="n")
rect(bb$pts[1], bb$pts[2], bb$pts[3], bb$pts[4], border="blue", lwd="2")
points(xy, pch=16, cex=1.5)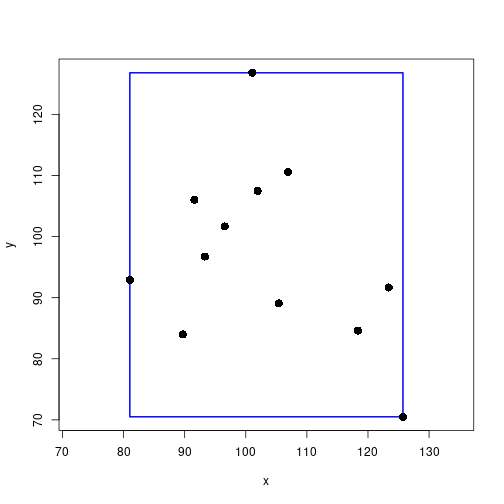
bb$width * bb$height[1] 2516.849Minimum bounding box
Rotating calipers algorithm
getMinBBox <- function(xy) {
stopifnot(is.matrix(xy), is.numeric(xy), nrow(xy) >= 2, ncol(xy) == 2)
## rotating calipers algorithm using the convex hull
H <- chull(xy) # hull indices, vertices ordered clockwise
n <- length(H) # number of hull vertices
hull <- xy[H, ] # hull vertices
## unit basis vectors for all subspaces spanned by the hull edges
hDir <- diff(rbind(hull, hull[1,])) # account for circular hull vertices
hLens <- sqrt(rowSums(hDir^2)) # length of basis vectors
huDir <- diag(1/hLens) %*% hDir # scaled to unit length
## unit basis vectors for the orthogonal subspaces
## rotation by 90 deg -> y' = x, x' = -y
ouDir <- cbind(-huDir[ , 2], huDir[ , 1])
## project hull vertices on the subspaces spanned by the hull edges, and on
## the subspaces spanned by their orthogonal complements - in subspace coords
projMat <- rbind(huDir, ouDir) %*% t(hull)
## range of projections and corresponding width/height of bounding rectangle
rangeH <- matrix(numeric(n*2), ncol=2) # hull edge
rangeO <- matrix(numeric(n*2), ncol=2) # orth subspace
widths <- numeric(n)
heights <- numeric(n)
for(i in seq(along=H)) {
rangeH[i, ] <- range(projMat[ i, ])
rangeO[i, ] <- range(projMat[n+i, ]) # orth subspace is in 2nd half
widths[i] <- abs(diff(rangeH[i, ]))
heights[i] <- abs(diff(rangeO[i, ]))
}
## extreme projections for min-area rect in subspace coordinates
eMin <- which.min(widths*heights) # hull edge leading to minimum-area
hProj <- rbind( rangeH[eMin, ], 0)
oProj <- rbind(0, rangeO[eMin, ])
## move projections to rectangle corners
hPts <- sweep(hProj, 1, oProj[ , 1], "+")
oPts <- sweep(hProj, 1, oProj[ , 2], "+")
## corners in standard coordinates, rows = x,y, columns = corners
## in combined (4x2)-matrix: reverse point order to be usable in polygon()
basis <- cbind(huDir[eMin, ], ouDir[eMin, ]) # basis formed by hull edge and orth
hCorn <- basis %*% hPts
oCorn <- basis %*% oPts
pts <- t(cbind(hCorn, oCorn[ , c(2, 1)]))
return(list(pts=pts, width=widths[eMin], height=heights[eMin]))
}Draw the minimum bounding box
mbb <- getMinBBox(xy) ## minimum bounding box
H <- chull(xy) ## convex hull
# plot original points, convex hull, and minimum bounding box
plot(xy, xlab="x", ylab="y", asp=1, type="n",
xlim=range(c(xy[ , 1], mbb$pts[ , 1])),
ylim=range(c(xy[ , 2], mbb$pts[ , 2])))
polygon(xy[H, ], col=NA) ## show convex hull
polygon(mbb$pts, border="blue", lwd=2)
points(xy, pch=16, cex=1.5)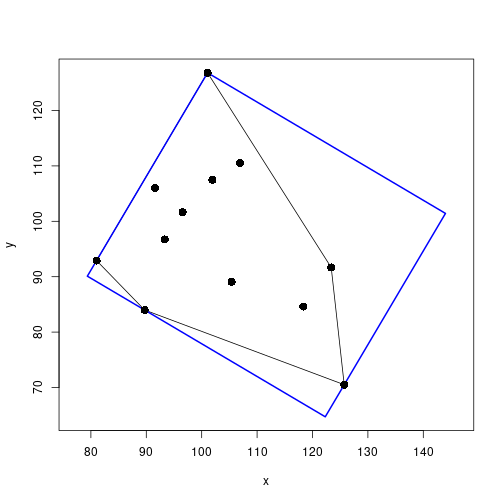
mbb$width * mbb$height ## box area[1] 2127.255Minimum enclosing circle
Skyum algorithm based on the convex hull
Circle defined by three points
getCircleFrom3 <- function(xy) {
stopifnot(is.matrix(xy), is.numeric(xy), nrow(xy) == 3, ncol(xy) == 2)
aa <- xy[1, ]
bb <- xy[2, ]
cc <- xy[3, ]
y <- xy[ , 2]
xDeltaA <- bb[1] - aa[1]
yDeltaA <- bb[2] - aa[2]
xDeltaB <- cc[1] - bb[1]
yDeltaB <- cc[2] - bb[2]
xDeltaC <- cc[1] - aa[1]
yDeltaC <- cc[2] - aa[2]
## check if the points are collinear: qr(xy)$rank == 1, or:
## determinant of difference matrix = 0, no need to use det()
dMat <- rbind(c(xDeltaA, yDeltaA), c(xDeltaB, yDeltaB))
if(isTRUE(all.equal(dMat[1,1]*dMat[2,2] - dMat[1,2]*dMat[2,1], 0, check.attributes=FALSE))) {
## define the circle as the one that's centered between the points
rangeX <- range(c(aa[1], bb[1], cc[1]))
rangeY <- range(c(aa[2], bb[2], cc[2]))
ctr <- c(rangeX[1] + 0.5*diff(rangeX), rangeY[1] + 0.5*diff(rangeY))
rad <- sqrt((0.5*diff(rangeX))^2 + (0.5*diff(rangeY))^2)
} else {
rad <- prod(dist(xy)) / (2 * abs(det(cbind(xy, 1)))) # circle radius
v1 <- rowSums(xy^2) # first vector in the numerator
v2x <- c( xDeltaB, -xDeltaC, xDeltaA) # 2nd vector numerator for Mx
v2y <- c(-yDeltaB, yDeltaC, -yDeltaA) # 2nd vector numerator for My
ctr <- c(t(v1) %*% v2y, t(v1) %*% v2x) / (2 * (t(y) %*% v2x)) # center
}
return(list(ctr=ctr, rad=rad))
}Vertex that produces the circle with the maximum radius
Used later in getMinCircle()
getMaxRad <- function(xy, S) {
stopifnot(is.matrix(xy), is.numeric(xy), nrow(xy) >= 2, ncol(xy) == 2)
stopifnot(is.numeric(S), length(S) >= 2, length(S) <= nrow(xy))
n <- length(S) # number of points
Sidx <- seq(along=S) # index for points
rads <- numeric(n) # radii for all circles
post <- (Sidx %% n) + 1 # next point in S
prev <- Sidx[order(post)] # previous point in S
for(i in Sidx) {
pts <- rbind(xy[S[prev[i]], ], xy[S[i], ], xy[S[post[i]], ])
rads[i] <- getCircleFrom3(pts)$rad # circle radius
}
return(which.max(rads))
}Check if the angle at B in triangle ABC exceeds 90 degrees
isBiggerThan90 <- function(xy) {
stopifnot(is.matrix(xy), is.numeric(xy), nrow(xy) == 3, ncol(xy) == 2)
d <- dist(xy)
dAB <- d[1]
dAC <- d[2]
dBC <- d[3]
return((dAB^2 + dBC^2 - dAC^2) < 0)
}Maximum pairwise distance between two 2D-points
getMaxPairDist <- function(xy) {
stopifnot(is.matrix(xy), is.numeric(xy), ncol(xy) == 2, nrow(xy) >= 2)
# 2D -> only convex hull is relevant
H <- chull(xy) # convex hull indices (vertices ordered clockwise)
pts <- xy[H, ] # points that make up the convex hull
N <- nrow(pts) # number of points on hull
dMat <- dist(pts, method="euclidean") # distance matrix
idx <- which.max(as.matrix(dMat)) # maximum distance
i <- (idx-1) %/% N+1 # column -> point 1
j <- (idx-1) %% N+1 # row -> point 2
mPts <- H[c(i, j)] # rows with max distance
dst <- max(dMat) # max distance
return(list(d=dst, idx=mPts))
}Minimal enclosing circle
getMinCircle <- function(xy) {
stopifnot(is.matrix(xy), is.numeric(xy), nrow(xy) >= 2, ncol(xy) == 2)
H <- chull(xy) # convex hull indices (vertices ordered clockwise)
hPts <- xy[H, ] # points that make up the convex hull
## min circle may touch convex hull in only two points
## if so, it is centered between the hull points with max distance
maxPD <- getMaxPairDist(hPts)
idx <- maxPD$idx # index of points with max distance
rad <- maxPD$d / 2 # half the distance -> radius
rangeX <- c(hPts[idx[1], 1], hPts[idx[2], 1])
rangeY <- c(hPts[idx[1], 2], hPts[idx[2], 2])
ctr <- c(rangeX[1] + 0.5*diff(rangeX), rangeY[1] + 0.5*diff(rangeY))
## check if circle centered between hPts[pt1Idx, ] and hPts[pt2Idx, ]
## contains all points (all distances <= rad)
dst2ctr <- dist(rbind(ctr, hPts[-idx, ])) # distances to center
if(all(as.matrix(dst2ctr)[-1, 1] <= rad)) { # if all <= rad, we're done
tri <- rbind(hPts[idx, ], ctr)
return(getCircleFrom3(tri))
}
## min circle touches hull in three points - Skyum algorithm
S <- H # copy of hull indices that will be changed
while(length(S) >= 2) {
n <- length(S) # number of remaining hull vertices
Sidx <- seq(along=S) # index for vertices
post <- (Sidx %% n) + 1 # next vertex in S
prev <- Sidx[order(post)] # previous vertex in S
mIdx <- getMaxRad(xy, S) # idx for maximum radius
## triangle where mIdx is vertex B in ABC
Smax <- rbind(xy[S[prev[mIdx]], ], xy[S[mIdx], ], xy[S[post[mIdx]], ])
## if there's only two hull vertices, we're done
if(n <= 2) { break }
## check if angle(ABC) is > 90
## if so, eliminate B - if not, we're done
if(isBiggerThan90(Smax)) { S <- S[-mIdx] } else { break }
}
return(getCircleFrom3(Smax))
}Draw the minimal enclosing circle
mc <- getMinCircle(xy)
angles <- seq(0, 2*pi, length.out=200)
circ <- cbind(mc$ctr[1] + mc$rad*cos(angles),
mc$ctr[2] + mc$rad*sin(angles))
# determine axis limits so that the circle will be visible
xLims <- mc$ctr[1] + c(-mc$rad, mc$rad)
yLims <- mc$ctr[2] + c(-mc$rad, mc$rad)
plot(xy, xlab="x", ylab="y", xlim=xLims, ylim=yLims, asp=1, type="n")
lines(circ, col="blue", lwd=2)
points(xy, pch=16, cex=1.5)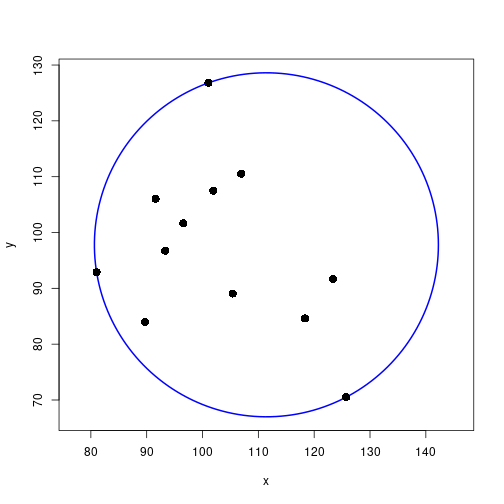
Get the article source from GitHub
R markdown - markdown - R code - all posts