Association tests and measures for ordered categorical variables
TODO
- link to correlation, association, diagCategorical
Install required packages
coin, mvtnorm, polycor, pROC, rms
wants <- c("coin", "mvtnorm", "polycor", "pROC", "rms")
has <- wants %in% rownames(installed.packages())
if(any(!has)) install.packages(wants[!has])Linear-by-linear association test
set.seed(123)
library(mvtnorm)
N <- 100
Sigma <- matrix(c(4,2,-3, 2,16,-1, -3,-1,9), byrow=TRUE, ncol=3)
mu <- c(-3, 2, 4)
Xdf <- data.frame(rmvnorm(n=N, mean=mu, sigma=Sigma))lOrd <- lapply(Xdf, function(x) {
cut(x, breaks=quantile(x), include.lowest=TRUE,
ordered=TRUE, labels=LETTERS[1:4]) })
dfOrd <- data.frame(lOrd)
matOrd <- data.matrix(dfOrd)cTab <- xtabs(~ X1 + X3, data=dfOrd)
addmargins(cTab) X3
X1 A B C D Sum
A 1 5 6 13 25
B 5 7 6 7 25
C 8 9 4 4 25
D 11 4 9 1 25
Sum 25 25 25 25 100library(coin)
lbl_test(cTab, distribution=approximate(B=9999))
Approximative Linear-by-Linear Association Test
data: X3 (ordered) by X1 (A < B < C < D)
chi-squared = 17.1325, p-value < 2.2e-16Polychoric and polyserial correlation
Polychoric correlation
library(polycor)
polychor(dfOrd$X1, dfOrd$X2, ML=TRUE)[1] 0.308646polychor(cTab, ML=TRUE)[1] -0.4818203Polyserial correlation
library(polycor)
polyserial(Xdf$X2, dfOrd$X3)[1] -0.1302779Heterogeneous correlation matrices
library(polycor)
Xdf2 <- rmvnorm(n=N, mean=mu, sigma=Sigma)
dfBoth <- cbind(Xdf2, dfOrd)
hetcor(dfBoth, ML=TRUE)
Maximum-Likelihood Estimates
Correlations/Type of Correlation:
1 2 3 X1 X2 X3
1 1 Pearson Pearson Polyserial Polyserial Polyserial
2 0.2792 1 Pearson Polyserial Polyserial Polyserial
3 -0.3899 -0.07191 1 Polyserial Polyserial Polyserial
X1 -0.05105 -0.1335 -0.07871 1 Polychoric Polychoric
X2 -0.1755 -0.2621 0.04899 0.3086 1 Polychoric
X3 -0.005707 -0.03443 -0.006209 -0.4818 -0.08556 1
Standard Errors:
1 2 3 X1 X2
1
2 0.09257
3 0.08522 0.09977
X1 0.1069 0.1044 0.1077
X2 0.1033 0.1001 0.1082 0.1062
X3 0.1071 0.1082 0.1088 0.09226 0.1132
n = 100
P-values for Tests of Bivariate Normality:
1 2 3 X1 X2
1
2 0.8156
3 0.6836 0.488
X1 0.107 0.5607 0.5548
X2 0.2 0.7338 0.2466 0.4721
X3 0.4423 0.9903 0.7281 0.3579 0.04774Association measures involving categorical and continuous variables
AUC, Kendall’s \(\tau_{a}\), Somers’ \(D_{xy}\), Goodman & Kruskal’s \(\gamma\)
One continuous variable and one dichotomous variable
N <- 100
x <- rnorm(N)
y <- x + rnorm(N, 0, 2)
yDi <- ifelse(y <= median(y), 0, 1)Nagelkerke’s pseudo-\(R^{2}\) (R2), area under the ROC-Kurve (C), Somers’ \(D_{xy}\) (Dxy), Goodman & Kruskal’s \(\gamma\) (Gamma), Kendall’s \(\tau\) (Tau-a)
library(rms)
lrm(yDi ~ x)$stats Obs Max Deriv Model L.R. d.f. P
1.000000e+02 4.370579e-07 5.974581e+00 1.000000e+00 1.451353e-02
C Dxy Gamma Tau-a R2
6.354000e-01 2.708000e-01 2.728738e-01 1.367677e-01 7.732807e-02
Brier g gr gp
2.356851e-01 5.793523e-01 1.784882e+00 1.379571e-01 Area under the ROC-curve (AUC)
library(pROC)
(rocRes <- roc(yDi ~ x, plot=TRUE, ci=TRUE, main="ROC-curve",
xlab="specificity (TN / (TN+FP))", ylab="sensitivity (TP / (TP+FN))"))
Call:
roc.formula(formula = yDi ~ x, plot = TRUE, ci = TRUE, main = "ROC-curve", xlab = "specificity (TN / (TN+FP))", ylab = "sensitivity (TP / (TP+FN))")
Data: x in 50 controls (yDi 0) < 50 cases (yDi 1).
Area under the curve: 0.634
95% CI: 0.5249-0.7431 (DeLong)rocCI <- ci.se(rocRes)
plot(rocCI, type="shape")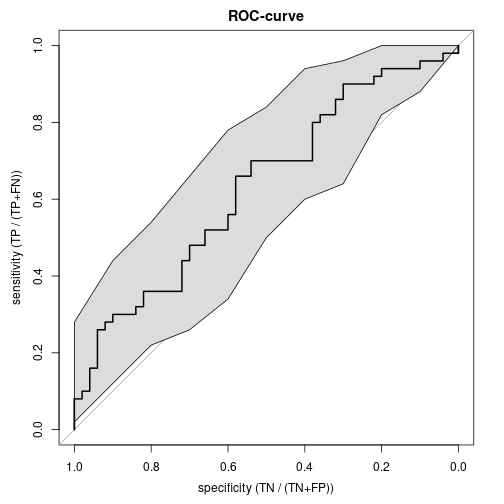
Detach (automatically) loaded packages (if possible)
try(detach(package:rms))
try(detach(package:Hmisc))
try(detach(package:grid))
try(detach(package:lattice))
try(detach(package:Formula))
try(detach(package:SparseM))
try(detach(package:pROC))
try(detach(package:polycor))
try(detach(package:sfsmisc))
try(detach(package:coin))
try(detach(package:survival))
try(detach(package:mvtnorm))
try(detach(package:splines))Get the article source from GitHub
R markdown - markdown - R code - all posts